LU Decompostion#
강좌: 수치해석
LU 분해 개요#
Gauss Elimination은 선형 방정식 \(Ax=b\) 를 Upper triangular matrix \(U\)를 이용한 \(Ux=c\) 로 바꿔서 푸는 방법이다.
이론적으로 \(A=LU\) 로 분해해서 푸는 것과 같다.
\[\begin{split}
Ax=LUx=b\\
Ux=c, Lc=b
\end{split}\]
\(A=LU\) 로 분해해놓으면 \(b\) 벡터가 달라져도 Substitution 과정만으로 빠르게 계산할 수 있다.
이론#
Gauss Elimination 과정을 Matrix Operation으로 생각하면 다음과 같다.
아래 예제를 생각하자.
\[\begin{split} A = \begin{bmatrix} 2 & 1 & 1 \\ 4 & 6 & 0 \\ -2 & 7 & 2 \end{bmatrix} \end{split}\]\(a_{21}\) 을 제거하기 위한 Row Operation (\((2) - 2\times(1)\)) 연산 Matrix
\[\begin{split} E_{21}=\left[\begin{array}{ccc} 1 & 0 & 0\\ -2 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]\end{split}\]\(a_{31}\) 을 제거하기 위한 Row Operation (\((3) + 1\times(1)\)) 연산 Matrix
\[\begin{split}E_{31}=\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ l & 0 & 1 \end{array}\right]\end{split}\]\(a_{32}\) 을 제거하기 위한 Row Operation (\((2) + 1\times(1)\)) 연산 Matrix
\[\begin{split}E_{32}=\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & l & 1 \end{array}\right]\end{split}\]
import numpy as np
def ematrix(n,i,j,d):
"""
Elimination matrix
Parameters
----------
n : integer
size of matrix
i : integer
row of pivot
j : intger
row of elimination
d : float
elimination coefficeint
Returns
-------
mat : array
elimination matrix
"""
# Make Identity matrix (size n)
mat = np.eye(n)
# Assign elimination coefficient
mat[j,i] = d
return mat
# Problem
A = np.array([[2,1,1],[4,-6,0],[-2,7,2]])
# One step (E21)
E21 = ematrix(3, 0, 1, -2)
print(E21 @ A)
[[ 2. 1. 1.]
[ 0. -8. -2.]
[-2. 7. 2.]]
# For all steps
E31 = ematrix(3, 0, 2, 1)
E32 = ematrix(3, 1, 2, 1)
U = E32 @ E31 @ E21 @ A
print(U)
[[ 2. 1. 1.]
[ 0. -8. -2.]
[ 0. 0. 1.]]
# Not commutative
E32 @ E31 @ E21 - E21 @ E31 @ E32
array([[ 0., 0., 0.],
[ 0., 0., 0.],
[-2., 0., 0.]])
\(E_{32} E_{31} E_{21} A = U\)
iE32 = ematrix(3, 1, 2, -1)
iE31 = ematrix(3, 0, 2, -1)
iE21 = ematrix(3, 0, 1, 2)
iE = iE21 @ iE31 @ iE32
print("Undo Gauss Eliminate")
print(iE @ U)
print("Lower Triangular matrix")
print(iE)
L =iE
Undo Gauss Eliminate
[[ 2. 1. 1.]
[ 4. -6. 0.]
[-2. 7. 2.]]
Lower Triangular matrix
[[ 1. 0. 0.]
[ 2. 1. 0.]
[-1. -1. 1.]]
LU decomposition
Formula
\[\begin{split} LU = \begin{bmatrix} u_{11} & u_{12} & u_{13} \\ 0 & u_{22} & u_{23} \\ 0 & 0 & u_{33} \\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ l_{21} & 1 & 0 \\ l_{31} & l_{23} & 1\\ \end{bmatrix} \end{split}\]\(l_{ij} = a'_{ij} / a'_{ii}\)
Save in a matrix
\[\begin{split} M = \begin{bmatrix} u_{11} & u_{12} & u_{13} \\ l_{21} & u_{22} & u_{23} \\ l_{31} & l_{23} & u_{33} \\ \end{bmatrix} \end{split}\]
Implementation#
Make \(A \rightarrow M\)
\[\begin{split} U = \left[\begin{array}{ccc} 2 & 1 & 1\\ 0 & -8 & -2\\ 0 & 0 & 1 \end{array}\right], L = \left[\begin{array}{ccc} 1 & 0 & 0\\ 2 & 1 & 0\\ -1 & -1 & 1 \end{array}\right] \end{split}\]\[\begin{split} M = \left[\begin{array}{ccc} 2 & 1 & 1\\ 2 & -8 & -2\\ -1 & -1 & 1 \end{array}\right], \end{split}\]
A = np.array([[2, 1, 1], [4, -6, 0], [-2, 7, 2]])
# First pivot a[0, 0]
# eliminate a[1, 0]
i = 0
j = 1
ratio = A[j, i] / A[i, i]
A[j, i] = ratio
A[j, i+1:] = A[j, i+1:] - ratio*A[i, i+1:]
print(ratio, A[j])
2.0 [ 2 -8 -2]
# eliminate a[2, 0]
j = 2
ratio = A[j, i] / A[i, i]
A[j, i] = ratio
A[j, i+1:] = A[j, i+1:] - ratio*A[i, i+1:]
print(ratio, A[j])
-1.0 [-1 8 3]
# next pivot a_{2,2}
# eliminate a_{3, 2}
i = 1
j = 2
ratio = A[j, i] / A[i, i]
A[j, i] = ratio
A[j, i+1:] = A[j, i+1:] - ratio*A[i, i+1:]
print(ratio, A[j])
-1.0 [-1 -1 1]
print(A)
[[ 2 1 1]
[ 2 -8 -2]
[-1 -1 1]]
Substibution
Forward : \(Lc=b\)
Backward: \(Ux=c\)
b = np.array([5, -2, 9])
# Forward (b to c)
# First row
b[0]
5
# Second row
b[1] = b[1] - A[1, 0]*b[0]
# Third row
i = 2
for j in range(i):
b[i] -= A[i, j]*b[j]
print(b)
[ 5 -12 2]
# Back substitution (Same as Gauss Elimination)
x = np.empty_like(b)
# Third row
i = 2
x[i] = b[i] / A[i,i]
# Second row
i = 1
x[i] = (b[i] - A[i, i+1]*x[i+1]) / A[i, i]
# First row
n = 3
i = 0
x[i] = b[i]
for j in range(i+1, n):
x[i] -= A[i, j]*x[j]
x[i] /= A[i,i]
print(x)
[1 1 2]
DIY#
다음 2개의 함수를 만드시오
LU 분해: LUdecomp
Substitution : LUsubs
역행렬#
역행렬은 \(Ax_i = e_i\) 를 푸는 과정이다.
\[
A X = I = A
\begin{bmatrix}
x_1 & x_2 & ... & x_n
\end{bmatrix} =
\begin{bmatrix}
e_1 & e_2 & ... & e_n
\end{bmatrix}
\]
예제#
다음 \(A\) 행렬의 역행렬을 구하시오.
\[\begin{split}
A = \begin{bmatrix}
2 & 1 & 1 \\
4 & 6 & 0 \\
-2 & 7 & 2
\end{bmatrix}
\end{split}\]
LU 분해 결과는 아래와 같다.
\[\begin{split}
M = \left[\begin{array}{ccc}
2 & 1 & 1\\
2 & -8 & -2\\
-1 & -1 & 1
\end{array}\right],
\end{split}\]
# LU 분해 결과 (이전 계산)
A = np.array([[ 2, 1, 1], [ 2, -8, -2], [-1, -1, 1]], dtype=np.float64)
# Allocate Identity and inverse Matrix
I = np.eye(3)
Ainv = np.empty_like(A)
# For first column
b = I[:, 0].copy()
x = Ainv[:, 0]
# Forward (b to c)
# Second row
b[1] = b[1] - A[1, 0]*b[0]
# Third row
i = 2
for j in range(i):
b[i] -= A[i, j]*b[j]
# Back substitution (Same as Gauss Elimination)
# Third row
i = 2
x[i] = b[i] / A[i,i]
# Second row
i = 1
x[i] = (b[i] - A[i, i+1]*x[i+1]) / A[i, i]
# First row
n = 3
i = 0
x[i] = b[i]
for j in range(i+1, n):
x[i] -= A[i, j]*x[j]
x[i] /= A[i,i]
print(x)
[ 0.75 0.5 -1. ]
# For first column
b = I[:, 1].copy()
x = Ainv[:, 1]
# Forward (b to c)
# Second row
b[1] = b[1] - A[1, 0]*b[0]
# Third row
i = 2
for j in range(i):
b[i] -= A[i, j]*b[j]
# Back substitution (Same as Gauss Elimination)
# Third row
i = 2
x[i] = b[i] / A[i,i]
# Second row
i = 1
x[i] = (b[i] - A[i, i+1]*x[i+1]) / A[i, i]
# First row
n = 3
i = 0
x[i] = b[i]
for j in range(i+1, n):
x[i] -= A[i, j]*x[j]
x[i] /= A[i,i]
print(x)
[-0.3125 -0.375 1. ]
# For first column
b = I[:, 2].copy()
x = Ainv[:, 2]
# Forward (b to c)
# Second row
b[1] = b[1] - A[1, 0]*b[0]
# Third row
i = 2
for j in range(i):
b[i] -= A[i, j]*b[j]
# Back substitution (Same as Gauss Elimination)
# Third row
i = 2
x[i] = b[i] / A[i,i]
# Second row
i = 1
x[i] = (b[i] - A[i, i+1]*x[i+1]) / A[i, i]
# First row
n = 3
i = 0
x[i] = b[i]
for j in range(i+1, n):
x[i] -= A[i, j]*x[j]
x[i] /= A[i,i]
print(x)
[-0.375 -0.25 1. ]
print(Ainv)
[[ 0.75 -0.3125 -0.375 ]
[ 0.5 -0.375 -0.25 ]
[-1. 1. 1. ]]
# Validate
A = np.array([[2,1,1],[4,-6,0],[-2,7,2]])
A @ Ainv
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
DIY#
앞서 만든 LU 분해 함수를 이용하여 역행렬 계산 함수를 만드시오
특수 행렬 분해#
Cholesky Decomposition#
\(LU\) 분해에서 \(U\) 행렬은 Diagonal 항과 Off-diagonal 항으로 분리할 수 있다.
\[ A = LU = LDU \]\(A\) 행렬이 대칭 (symmetric) 일 경우 다음 관계를 만족한다.
\[\begin{split} A = A^T \\ LDU = (LDU)^T = U^T D L^T \end{split}\]즉 \(L = U^T\) 를 만족한다.
\(A=LDL^T\)
Cholesky 분해법
A 가 Positive Definite 일 때 (symmetric, all positive pivots)
\[ A = LDL^T = (LD^{1/2}) (D^{1/2} L^T) = (LD^{1/2}) (LD^{1/2})^T \]구현
\[\begin{split} \begin{align} l_{ki} &= \frac{a_{ki} - \sum_{j=1}^{i-1} l_{ij} l_{kj}}{l_{ii}} \textrm{ for } i=1,2,...k-1 \\ l_{kk} &= \sqrt{a_{kk} - \sum_{j=1}^{k-1} l_{kj}^2} \end{align} \end{split}\]
예제#
다음 대칭 행렬을 Cholesky 분해하시오.
\[\begin{split}
A = \begin{bmatrix}
6 & 15 & 55 \\
15 & 55 & 225 \\
55 & 225 & 979
\end{bmatrix}
\end{split}\]
A = np.array([[6, 15, 55], [15, 55, 225], [55, 225, 979]], dtype=np.float64)
L = np.zeros_like(A)
# first row
k = 0
L[k, k] = np.sqrt(A[k, k])
# Second row
k = 1
i = 0
L[k, i] = A[k, i] / L[i, i]
L[k, k] = np.sqrt(A[k, k] - L[k, i]**2)
# Third row
k = 2
i = 0
L[k, i] = A[k, i] / L[i, i]
i = 1
L[k, i] = (A[k, i] - sum(L[i, j]*L[k, j] for j in range(i)))/L[i,i]
L[k ,k] = np.sqrt(A[k, k] - sum(L[k, j]**2 for j in range(k)))
L
array([[ 2.44948974, 0. , 0. ],
[ 6.12372436, 4.18330013, 0. ],
[22.45365598, 20.91650066, 6.11010093]])
# Validate
L @ L.T
array([[ 6., 15., 55.],
[ 15., 55., 225.],
[ 55., 225., 979.]])
LU decomposition과 비교
# LU decomposition
M = A.copy()
i = 0
j = 1
ratio = M[j, i] / M[i, i]
M[j, i] = ratio
M[j, i+1:] = A[j, i+1:] - ratio*M[i, i+1:]
j = 2
ratio = M[j, i] / M[i, i]
M[j, i] = ratio
M[j, i+1:] = M[j, i+1:] - ratio*M[i, i+1:]
i = 1
j = 2
ratio = M[j, i] / M[i, i]
M[j, i] = rati
M[j, i+1:] = M[j, i+1:] - ratio*M[i, i+1:]
print(M)
[[ 6. 15. 55. ]
[ 2.5 17.5 87.5 ]
[ 9.16666667 5. 37.33333333]]
\(A = LU=LDU'\) $\( L = \begin{bmatrix} 1 & 0 & 0 \\ 2.5 & 1 & 0 \\ 9.1667 & 5 & 1 \end{bmatrix} U = \begin{bmatrix} 6 & 1.5 & 55 \\ 0 & 17.5 & 87.5 \\ 0 & 0 & 37.3333 \end{bmatrix} = \begin{bmatrix} 6 & 0 & 0 \\ 0 & 17.5 & 0 \\ 0 & 0& 37.3333 \end{bmatrix} \begin{bmatrix} 1 & 2.5 & 9.1667 \\ 0 & 1 & 5 \\ 0 & 0 & 1 \end{bmatrix} \)$
\(L\sqrt{D}\) $\( L \sqrt{D} = \begin{bmatrix} \sqrt{6} & 0 & 0 \\ 2.5 \sqrt{6} & \sqrt{17.5} & 0 \\ 9.1667 \sqrt{6} & 5 \sqrt{17.5} & \sqrt{37.3333} \end{bmatrix} \)$
삼중대각 행렬#
삼중 대각 행렬 (Tri-diagonal matrix)는 Diagonal과 그 바로 옆에 1개씩만 값이 있는, 즉 3의 대역폭을 갖는 행렬이다.
실제 편미분 방정식 해석에서 자주 보이는 행렬이다.
\[\begin{split}
\begin{bmatrix}
b_1 & c_1 & & & & & \\
a_2 & b_2 & c_2 & & & & \\
& a_3 & b_3 & c_3 & & & \\
& & & & & & & \\
& & & & a_{n-1} & b_{n-1} & c_{n-1} \\
& & & & & a_{n} & b_{n}
\end{bmatrix}
\begin{bmatrix}
x_1 \\ x_2 \\ x_3 \\ \\ x_{n-1} \\ x_n
\end{bmatrix}
\begin{bmatrix}
d_1 \\ d_2 \\ d_3 \\ \\ d_{n-1} \\ d_n
\end{bmatrix}
\end{split}\]
(LU Decomposition + Forward substitution), Backward substitution 으로 효과적으로 계산할 수 있다.
Algorithm
For \(i = 2, 3,...,n\)
\[\begin{split} \begin{align} w &= \frac{a_i}{b_{i-1}} \\ b_i &= b_i - w c_{i-1} \\ d_i &= d_i - w d_{i-1} \end{align} \end{split}\]Back substitution
\[\begin{split} \begin{align} x_n &= \frac{d_n}{b_n} \\ x_i & = \frac{d_i - c_i x_{i+1}}{b_i} \textrm{ for } i=n-1, n-2,...,1 \end{align} \end{split}\]
예제#
아래 삼중대각 행렬의 해를 구하시오.
\[\begin{split}
\begin{bmatrix}
2.04 & -1 & & \\
-1 & 2.04 & -1 & \\
& -1 & 2.04 & -1 \\
& & -1 & 2.04
\end{bmatrix}
T
=
\begin{bmatrix}
40.8 \\ 0.8 \\ 0.8 \\ 200.8
\end{bmatrix}
\end{split}\]
A = np.array([[2.04, -1, 0, 0], [-1, 2.04, -1, 0], [0, -1, 2.04, -1], [0, 0, -1, 2.04]])
d = np.array([40.8, 0.8, 0.8, 200.8])
A
array([[ 2.04, -1. , 0. , 0. ],
[-1. , 2.04, -1. , 0. ],
[ 0. , -1. , 2.04, -1. ],
[ 0. , 0. , -1. , 2.04]])
a = np.array([0., -1., -1. , -1.])
b = np.array([2.04, 2.04, 2.04, 2.04])
c = np.array([-1., -1., -1., 0.])
n = len(a)
x = np.empty_like(a)
# Forward sweep
for i in range(1, n):
w = a[i] / b[i-1]
b[i] -= w*c[i-1]
d[i] -= w*d[i-1]
# Backward sweep
x[-1] = d[-1] / b[-1]
for i in range(n-2, -1, -1):
x[i] = (d[i] - c[i]*x[i+1]) / b[i]
# Solution
x
array([ 65.96983437, 93.77846211, 124.53822833, 159.47952369])
# Validation
A @ x
array([ 40.8, 0.8, 0.8, 200.8])
DIY#
Cholesky 분해 계산 함수를 만드시오.
삼중 대각 행렬 계산 함수를 만드시오.
Scipy 활용#
scipy.linalg 모듈은 다양한 행렬 계산 알고리즘을 제공함
numpy.linalg는 제한된 기능을 제공
참고
Solve linear system#
linalg.solve: \(Ax=b\) 해석linalg.inv: \(A^{-1}\) 계산linalg.det: \(det(A)\) 계산linalg.norm: 벡터, 행렬의 Norm 계산
Decomposition#
LU (Lower Upper) Decomposition
Singual Value Decomposition (SVD)
QR Decomposition
Eigenvalue#
linalg.eig: Eigenvalue, Eigenvector 계산\(Ax = \lambda x\)
np.linalg.solve?
예제#
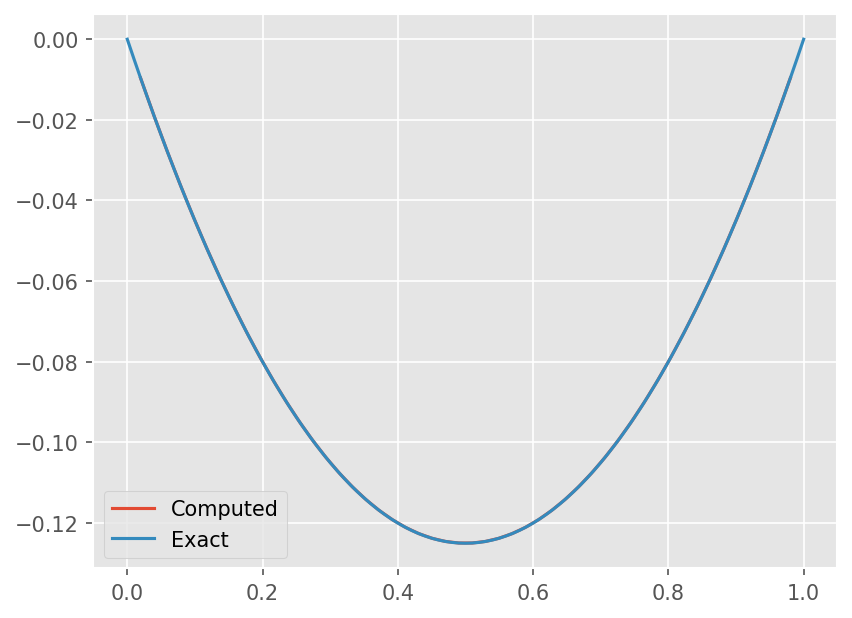
양 끝단이 고정된 보의 방정식은 다음과 같다.
\[
u''(x) = 1, u(0) = 0, u(1) = 0.
\]
이 미분방정식의 이론해는 다음과 같다.
\[
u(x) = -\frac{1}{2}x + \frac{1}{2}x^2.
\]
수치적으로 이를 해석하는 경우 \([0,1]\) 구간을 n 등분하고, 각 지점의 값을 \(u_i = u(x_i)\) 라 하면 위 미분 방정식으 다음 형태로 바뀐다.
\[\begin{split}\frac{1}{\Delta x^2}
\begin{bmatrix}
-2 & 1 & 0 &... &0 \\
1 & -2& 1 & 0 ... & 0 \\
0 & 1 & -2 & 1 ... & 0 \\
... & ... & ... & ... & ... \\
0 & 0 & 1 & -2 & 1 \\
0 & 0 & 0 & 1 & -2
\end{bmatrix}
\begin{bmatrix}
u_1 \\
u_2 \\
u_3 \\
... \\
u_{n-2} \\
u_{n-1}
\end{bmatrix}
= \begin{bmatrix}
f(x_1) \\
f(x_2) \\
f(x_3) \\
... \\
f(x_{n-2})\\
f(x_{n-1})\\
\end{bmatrix}
\end{split}\]
이 문제를 수치적으로 해석해보자.
# Number of division
n = 51
x = np.linspace(0, 1, n+1)
h = np.diff(x)[0]
# Matrix system
A = np.diag([-2]*(n-1)) + np.diag([1]*(n-2), -1) + np.diag([1]*(n-2), 1)
b = np.array([1]*(n-1))*h**2
np.diag([-2]*(n-1)), np.diag([1]*(n-2), -1), np.diag([1]*(n-2), 1)
(array([[-2, 0, 0, 0],
[ 0, -2, 0, 0],
[ 0, 0, -2, 0],
[ 0, 0, 0, -2]]),
array([[0, 0, 0, 0],
[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0]]),
array([[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1],
[0, 0, 0, 0]]))
# Solve
#u = np.linalg.solve(A, b)
from scipy import linalg
u = linalg.solve(A, b)
%matplotlib inline
from matplotlib import pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.dpi'] = 150
plt.plot(x[1:-1], u)
xe = np.linspace(0, 1, 101)
plt.plot(xe, -0.5*xe + 0.5*xe**2)
plt.legend(["Computed", "Exact"])
<matplotlib.legend.Legend at 0x7f4267518410>
